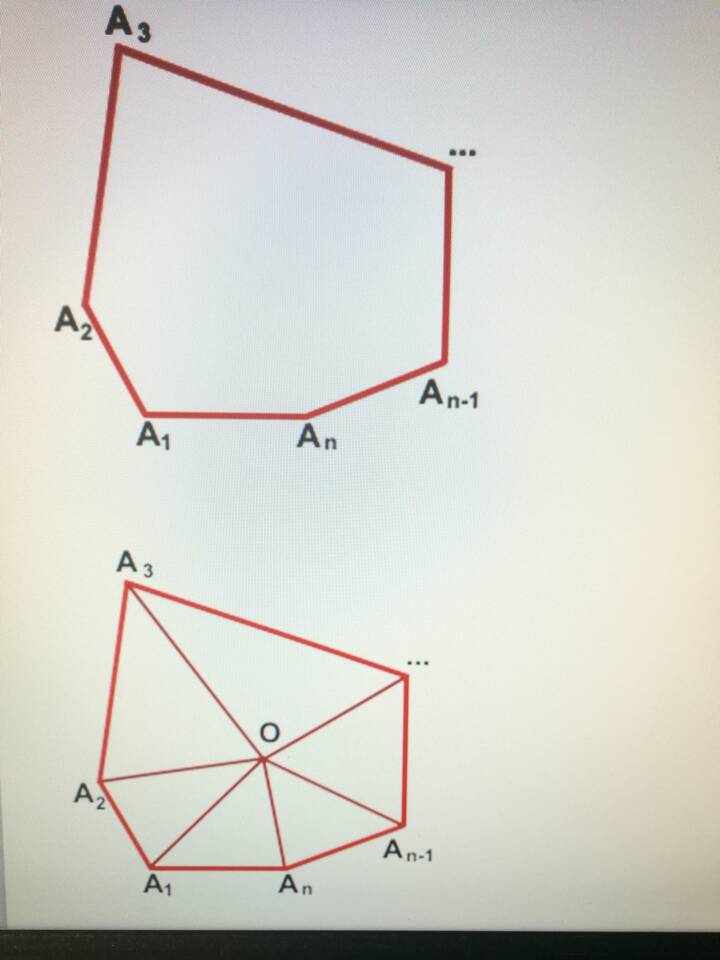
Сумма углов выпуклого многоугольника является важной характеристикой в геометрии. Для двадцатисемиугольника (27-угольника) эта величина может быть точно вычислена по общей формуле для выпуклых n-угольников.
Содержание
Формула суммы углов выпуклого n-угольника
- Основная формула: S = (n - 2) × 180°
- Где n - количество сторон (углов) многоугольника
- Для 27-угольника: n = 27
Расчет суммы углов для 27-угольника
| Шаг расчета | Вычисление |
| 1. Определение количества сторон | n = 27 |
| 2. Подстановка в формулу | S = (27 - 2) × 180° |
| 3. Вычисление разности | 27 - 2 = 25 |
| 4. Окончательный расчет | S = 25 × 180° = 4500° |
Проверка правильности расчета
- Для треугольника (3-угольника): (3-2)×180° = 180° - верно
- Для четырехугольника: (4-2)×180° = 360° - верно
- Для пятиугольника: (5-2)×180° = 540° - верно
- Следовательно, формула работает и для 27-угольника
Значение результата
- Сумма всех внутренних углов равна 4500 градусов
- Средняя величина одного угла: 4500° / 27 ≈ 166,67°
- Для правильного 27-угольника каждый угол равен ≈ 166,67°
Практическое применение
Знание суммы углов многоугольника важно для:
- Конструирования геометрических объектов
- Решения задач по геометрии
- Компьютерного моделирования
- Архитектурных расчетов
Дополнительные свойства
Для любого выпуклого n-угольника:
1) Количество диагоналей: n(n-3)/2 = 324
2) Сумма внешних углов всегда равна 360°
Эти свойства помогают в комплексном анализе геометрических фигур.