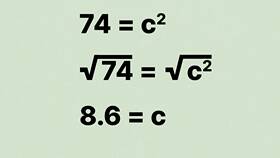В геометрии существует несколько фундаментальных теорем, связанных с суммой площадей различных фигур. Рассмотрим основные доказательства этих утверждений.
Содержание
Теорема Пифагора через суммы площадей
Классическое доказательство теоремы Пифагора основано на сравнении площадей:
- Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c
- Построим квадрат со стороной (a+b)
- Площадь большого квадрата можно выразить двумя способами:
- Как (a+b)² = a² + 2ab + b²
- Как сумму площади 4 треугольников и площади квадрата со стороной c: 4*(ab/2) + c² = 2ab + c²
- Приравнивая выражения: a² + 2ab + b² = 2ab + c²
- После сокращения получаем: a² + b² = c²
Сумма площадей в параллелограмме
| Утверждение | Доказательство |
| Площадь параллелограмма равна сумме площадей двух треугольников | Диагональ делит параллелограмм на два равных треугольника, поэтому S = 2*(1/2*a*h) = a*h |
Свойство площадей подобных фигур
Если линейные размеры фигуры увеличиваются в k раз, то площадь увеличивается в k² раз:
- Для квадрата: (k*a)² = k²*a²
- Для прямоугольника: (k*a)*(k*b) = k²*(a*b)
- Для треугольника: (k*a*k*h)/2 = k²*(a*h/2)
Площадь круга как сумма площадей
Метод Архимеда:
- Разобьем круг на множество узких секторов
- Каждый сектор приближенно равен треугольнику
- Сумма площадей всех треугольников: Σ(1/2*r*r*Δθ) = 1/2*r²*ΣΔθ
- При Δθ→0, ΣΔθ→2π
- Итого: S = 1/2*r²*2π = πr²
Сравнение площадей через интегралы
Для непрерывных функций площадь под кривой равна определенному интегралу:
| Функция | Площадь |
| f(x) на [a,b] | S = ∫abf(x)dx |
| Между двумя кривыми | S = ∫ab(f(x)-g(x))dx |
Принцип Кавальери
Если при пересечении двух тел любой плоскостью получаются фигуры равной площади, то объемы тел равны. Аналогично для площадей:
- Если при пересечении любой прямой получаются отрезки равной длины
- То площади фигур равны
- Это позволяет сравнивать площади сложных фигур
Площадь поверхности сложных тел
Площадь поверхности можно представить как сумму:
- Для призмы: сумма площадей боковых граней + 2 основания
- Для пирамиды: сумма площадей треугольных граней + основание
- Для цилиндра: 2πr² + 2πrh
- Для сферы: 4πr² (предел суммы площадей малых элементов)